Climate Science
Milankovitch Cycles and Climate: Part II – Orbital Eccentricity, Apsidal Precession and Orbital Inclination
In part I, we looked at some of the ways in which changes in axial obliquity and precession can affect the climate. In this article, we’ll look at orbital eccentricity, apsidal precession and orbital inclination, and some of their climatological consequences.
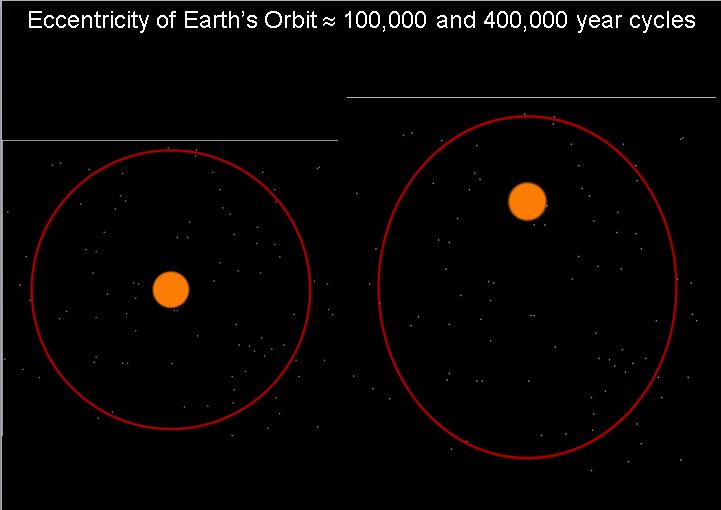
Orbital Eccentricity:
This refers how elliptical earth’s orbital path is. The greater the eccentricity of a planet’s orbital path, the less circle-like and more elliptical (oval-like) it is. An ellipse has an eccentricity greater than or equal to zero, but less than one. An eccentricity value of e = 0 corresponds to a perfect circle, whereas e = 1 corresponds to a parabola, and e > 1 corresponds to a hyperbola. At higher eccentricity values (albeit less than one), there is a greater discrepancy between a planet’s perihelion and aphelion: a planet’s nearest and furthest points from the Sun during its orbit. (more…)