Milankovitch Cycles

Milankovitch Cycles and Climate: Part III – Putting it All Together

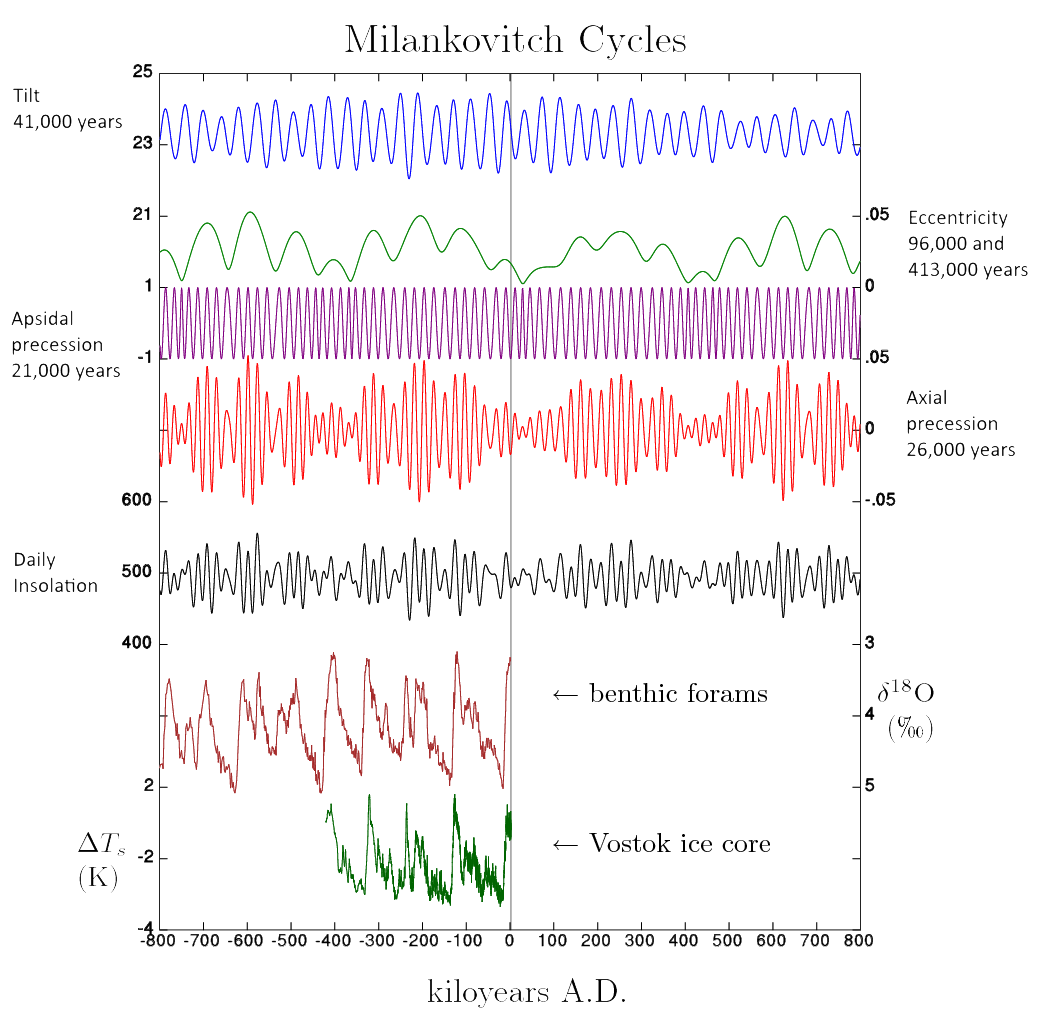
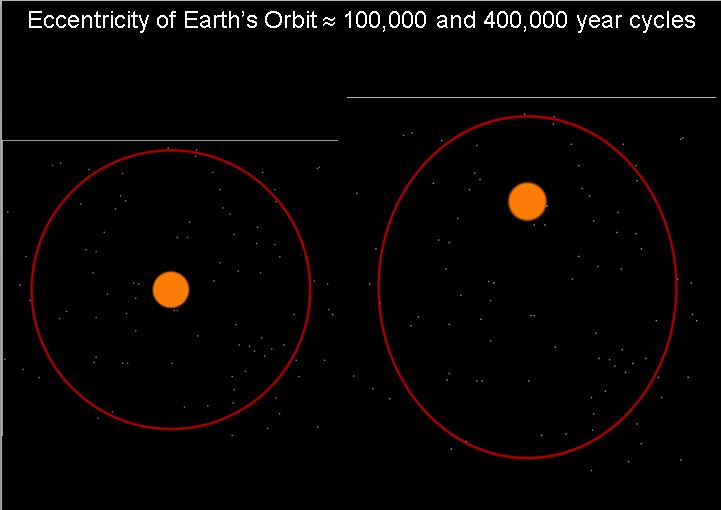
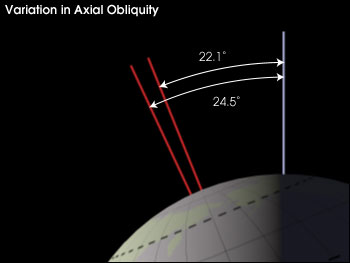
In parts I and II, we looked at axial obliquity, axial precession, apsidal precession, orbital eccentricity and orbital inclination, and how their cycles can affect the climate. In this installment of the series, we’ll look briefly at how these cycles look when combined, and then discuss one of the most prominent unsolved problems raised by the theory: The 100,000 Year problem.

Putting it all together

Putting it all together

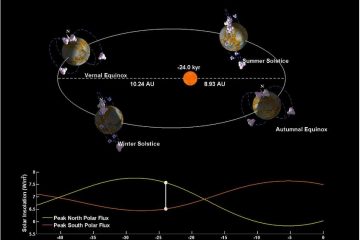
Notice that the peaks and valleys in temperature are roughly periodic, and that with the possible exception of apsidal precession, there are slight fluctuations in the periods and amplitudes of these orbital cycles. One reason for this has to do with fluctuations in solar output, but another likely reason has to do with the very causes of these orbital cycles themselves: namely, these cycles are driven by mutual gravitational perturbations between the Earth, Sun, Moon, and to a lesser extent, Jupiter and the other planets in the solar system (Borisenkov 1985, Spiegel 2010) . (more…)

Share
By Credible Hulk, ago

Milankovitch Cycles and Climate: Part II – Orbital Eccentricity, Apsidal Precession and Orbital Inclination

In part I, we looked at some of the ways in which changes in axial obliquity and precession can affect the climate. In this article, we’ll look at orbital eccentricity, apsidal precession and orbital inclination, and some of their climatological consequences.

Orbital Eccentricity:

This refers how elliptical earth’s orbital path is. The greater the eccentricity of a planet’s orbital path, the less circle-like and more elliptical (oval-like) it is. An ellipse has an eccentricity greater than or equal to zero, but less than one. An eccentricity value of e = 0 corresponds to a perfect circle, whereas e = 1 corresponds to a parabola, and e > 1 corresponds to a hyperbola. At higher eccentricity values (albeit less than one), there is a greater discrepancy between a planet’s perihelion and aphelion: a planet’s nearest and furthest points from the Sun during its orbit. (more…)

Share
By Credible Hulk, ago

Milankovitch Cycles and Climate: Part I – Axial Tilt and Precession

The theory of Milankovitch cycles is named after Serbian astronomer and geophysicist, Milutin Milanković, who in the 1920s postulated three cyclical movement patterns related to Earth’s orbit and rotation and their resultant effects on the Earth’s climate. These cycles include axial tilt (obliquity), elliptical eccentricity, and axial precession. In aggregate, these cycles contribute to profound long term changes in earth’s climate via orbital forcing.

Axial Obliquity:

The Earth’s rotational axis is always tilted slightly; currently, its axis is about 23.4 degrees from the vertical. Alternatively, you could say that its equatorial plane is tilted about 23.4 degrees relative to its orbital plane. This tilt is responsible for Earth’s seasons. During the Northern Hemisphere (NH) summer, Earth is further away from the Sun than it is during the NH winter due to its slightly elliptical orbit, yet it receives more sunlight because it’s tilted towards the Sun. During this same time period, the Southern Hemisphere (SH) is tilted away from the Sun, which is why NH summer coincides with SH Winter and vice versa. Contrastingly, during the NH winter, the Earth is closer to the Sun, yet receives less sunlight because it’s tilted away from it. During that same period, the SH is tilted towards the Sun, and is thus experiencing summer. (more…)

Share
By Credible Hulk, ago