Heat, and internal energy
In a recent article, I mentioned in passing that the internal energy of a system is a state function. Just to quickly recap, state functions are properties of a physical system whose values do not depend on how they were arrived at from a prior state of the system. They depend only on the starting and ending states of the system.
I then contrasted state functions with path-dependent functions, which can take on very different values depending on the path by which the system arrived at its current state from its previous state (the history of the system matters).
Perhaps counter-intuitively, while it’s true that internal energy is a state function, the change in a system’s internal energy is the sum of two path-dependent functions.
Specifically, ΔE = q + w (1),
where q is the heat transferred, and w is the work done on the system by the environment. Heat simply refers to the thermal energy transferred across the system boundary, and internal energy refers to the total energy (kinetic plus potential) of the system.
As the name implies, internal energy includes the interactions and relative motions among the particles of a given system, and does not include interactions and motions relative to objects outside the system (Stowe 2008).
Quantum effects constrain individual molecules to discrete allowed energy levels, and a more detailed statistical thermodynamic approach would account for rotational and vibrational energy modes, in addition to translational and potential energy, and would even entail different microstate-counting methods for fermions vs bosons (Stowe 2008). However, I am choosing to use a more coarse-grained description for present purposes.
So, for now, you can just think of internal energy as the total kinetic plus potential energy of the particles comprising a physical system, and heat as thermal energy transferred to the system from the environment or vice versa. Hence, heat transferred to the system from its surrounding environment (q > 0) raises the internal energy of the system, whereas heat transferred from the system to its surrounding environment (q < 0) lowers it.
Work
Recall that in classical physics, the work done by a force on an object refers to the path integral of the inner product (or dot product) of the force on the object with the path along which the object is being pushed. It is generally path dependent. If you doubt this, try moving a piece of furniture directly from your bedroom to your kitchen, vs carrying it around the block 10 times before bringing it back and setting it in that same spot in the kitchen. Strictly, speaking, there are special cases in which work can be treated as a state function, such as when the only forces acting on an object are what we call “conservative forces,” but in general work cannot be treated as a state variable (Taylor 2005). In fact, part of the definitional criteria a force must satisfy to be conservative is that the work it does must be path independent. The other criterion is that the force must depend only on the particle’s position, and not on its velocity or any other variable (Taylor 2005).
Note that here again I am using the convention in which positive q represents thermal energy transferred in to the system from the environment, and positive w represents positive work done on the system by an external force. By extension, negative q and w represent heat transferred from the system and work done by the system respectively. So, when q and w are both positive, so is ΔE. When q and w are both negative, so is ΔE. When one is positive and one is negative, the sign ΔE of depends on the respective magnitudes of q and w.
Work by an Ideal Gas at Constant Temperature
To make this more concrete, supposing your system is an ideal gas obeying the relationship PV = nRT, where P = pressure, V = volume, n = the number of moles of your gas, R is the gas constant, and T = temperature. Let us also suppose that we need only concern ourselves with P-V work (work corresponding to changes in pressure and/or volume), and that T is constant (called an isothermal process). If the system goes from a state Pi, Vi, to a state Pf, Vf, (where ![]() ), then the work in this case is quantified by
), then the work in this case is quantified by
which means
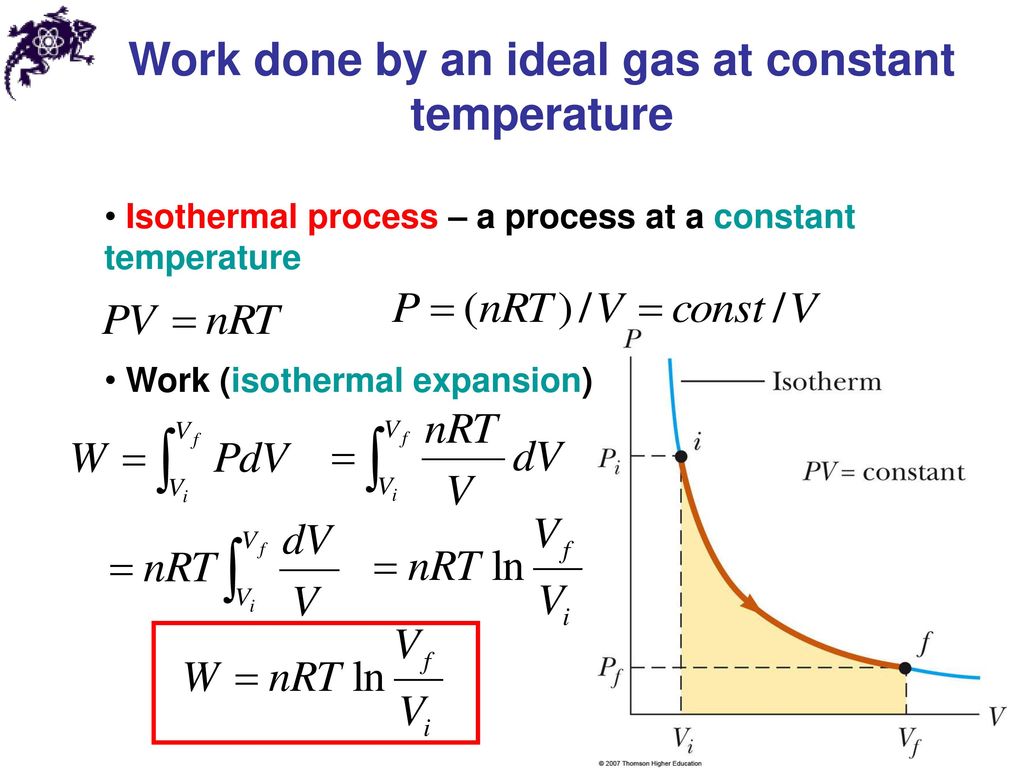
Image source here
(isothermal expansion), which means it would be negative work as per our convention.
Substituting equation (3) into (1) leads to 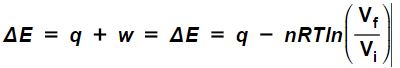 .
.
I should probably mention that in this case that the work done by the system would be perfectly off-set by the heat absorbed by the system, and thus the total change in internal energy ΔE would equal zero. This is because we used an isothermal process with an ideal gas, and one of the assumptions of the ideal gas model is a lack of intermolecular interactions between the particles comprising the gas, which is not the case with real gases. What that means is that there’s no potential energy resulting from electrostatic forces between the gas particles, so the internal energy is entirely kinetic. And since temperature is proportional to the average molecular kinetic energy of a system, constant temperature implies constant internal energy for processes involving ideal gasses. Keep in mind that this is not generally the case for non-ideal gasses.
Reversibility
Before moving on, I should also mention that the above change of state calculation demonstrates the concept of a reversible path. Reversibility just refers to an idealized concept used in thermodynamic theory in which changes of state are carried out in such a manner that the system and its surroundings are only out of equilibrium by an infinitesimal amount. In practice, we can’t really do that. It’s just hypothetical, but it’s a useful concept nevertheless.
Work by an Ideal Gas at Constant Pressure
In contrast, suppose a change between those same two starting and ending states were carried out via a change in volume at constant external pressure (called an isobaric process), followed by a change in pressure at constant volume (called an isovolumetric process). In this case, since no work is done during the isovolumetric portion of the process, the work is quantified by
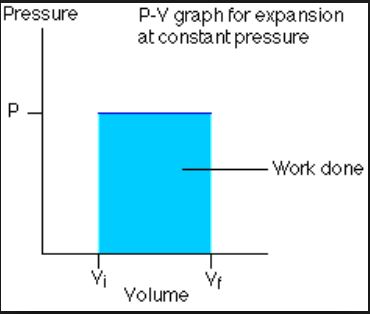
Image c/o Boston University
Despite starting and ending at the same states, these paths lead to very different values for the work done. In general, it’s nearly impossible to know the precise path by which every state change in a complicated system was arrived at, so scientists and engineers find it useful to deal primarily with state functions whenever possible. Enter enthalpy.
References
1st Law of Thermodynamics. (2013). Chemistry LibreTexts. Retrieved 3 July 2018, from https://goo.gl/3C7Lcu
An Introduction to Thermodynamics and Statistical Mechanics. 2nd ed. (2008). Google Books. Retrieved 3 July 2018, from https://goo.gl/4h3Wtp
Line Integrals of Vector Fields. (2018). Math.oregonstate.edu. Retrieved 3 July 2018, from https://math.oregonstate.edu/home/programs/undergrad/CalculusQuestStudyGuides/vcalc/lvec/lvec.html
Taylor, J. R. (2005). Classical mechanics. University Science Books. Retrieved 3 July 2018, from https://goo.gl/PzqEth
Isothermal Processes. (2018). Hyperphysics.phy-astr.gsu.edu. Retrieved 3 July 2018, from http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/isoth.html
4.3 Features of reversible processes . (2018). Web.mit.edu. Retrieved 3 July 2018, from http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node34.html
Work. (2013). Chemistry LibreTexts. Retrieved 3 July 2018, from https://goo.gl/isR89x
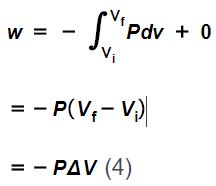
1 Comment
Enthalpy: Exothermic vs Endothermic Processes – The Credible Hulk · July 8, 2018 at 8:46 am
[…] recently, I wrote another one in which I talked about heat, work, reversibility, and internal energy in thermodynamic […]
Comments are closed.