Dipole-dipole interactions
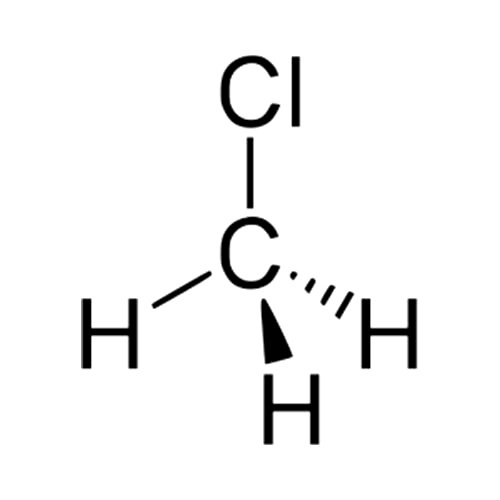
Many covalently bonded molecules have a net neutral electric charge, but do not distribute their charge evenly. Some parts of their structure have greater electron density than others. This is again a result of differences in electronegativity. For example, chlorine is more electronegative than carbon. Consequently, bonds between C and Cl are polar bonds. In contrast with non-polar covalent bonds, in which case electron density is shared roughly equally between two bonded atoms, polar bonds are simply covalent bonds across which the electric charge is not evenly distributed. In the case of a C-Cl bond, the Cl will have a partially negative charge and the C will have a partially positive charge, even if the molecule’s net charge is neutral. For example, consider the molecule chloromethane (aka methyl chloride):
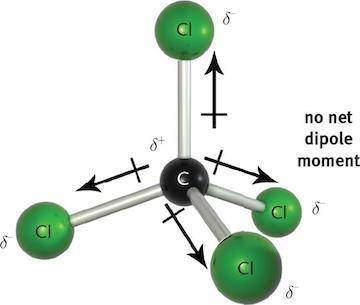
It’s a C atom covalently bonded to a Cl and three hydrogens. C and H have similar electronegativities, but Cl has a much higher electronegativity. As a result, we say this molecule has a dipole moment. The presence of a polar bond doesn’t guarantee that a molecule will itself be polar, however. Whether such a molecule is polar depends on the geometry of the compound, the presence or lack of additional polar bonds, and their spatial orientation. There are indeed cases in which the vector sum of all the dipole moments resulting from two or more polar bonds in a compound will cancel each other out, resulting in a non-polar molecule.
Carbon tetrachloride is an example of this. Notice how the vectors representing the electric dipole cancel each other out because of the tetrahedral geometry of CCl4. That said, dipole-dipole interactions between polar molecules are incredibly important in chemistry, biology, and biochemistry due to their resulting electrostatic interactions with one another, and they strongly influence the bulk properties of a given chemical substance or mixture.
Polarity can even be quantified by defining a quantity called a dipole moment (µ) as an indicator of polarity, such that µ is a vector quantity equal to the amount of partial charge (q) on either end of the dipole multiplied by a vector (d) representing their distance of separation (Klein 2015):
µ = qd.
Here µ has units of electric charge times distance, in which case it is convenient to introduce a new called a Debye (D), which is defined as 1 debye = 10-18 esu*cm, where esu stands for electrostatic units (a unit of electric charge used within the CGS unit system). Just to get an idea of scale here, the electron has a charge of -4.80*10-10 esu (Klein Pg. 29-30).
Consequently, since most partial charges on dipoles are on the order of 10-10 esu, and their distances generally on the order of 10-8 cm, most polar molecules will have dipole moments somewhere on the order of 10-10 esu times 10-8 cm = 10-18 esu*cm. It’s no coincidence that this works out to 1 debye (hence the convenience of introducing the new unit).
For example, the chloromethane molecule is a relatively simple case due to having only one polar bond, and it is reported to have a dipole moment of 1.87 D. The dipole moment can also be used to quantify the percent ionic character of different bonds, which is tangential to the focus of this post, but which you can read about here if you’d like.
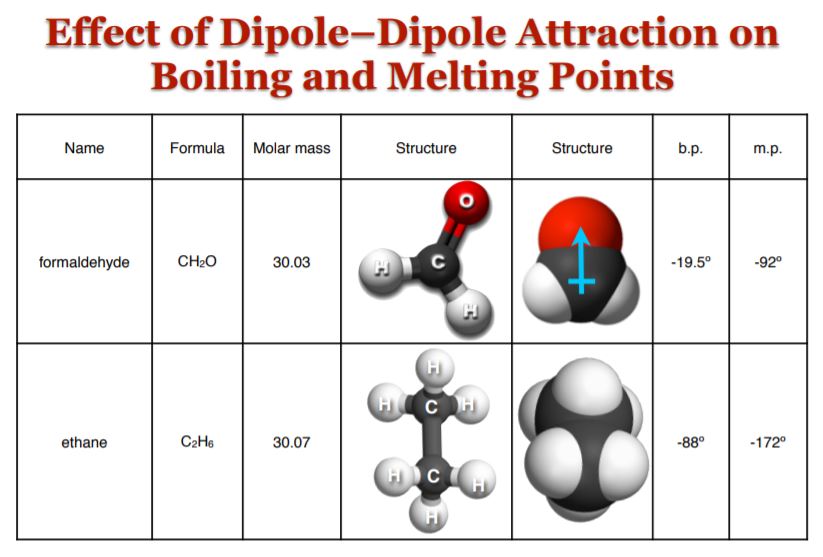
Dipole interactions also affect boiling and melting points. The graphic below depicts two molecules of similar mass: formaldehyde and ethane. However, despite this, the former has much higher boiling and melting points than the latter, and the reason is attributed to its distinct dipole moment of its carbonyl group:
You might be thinking that the repulsive interactions between parts of neighboring molecules with like charges ought to “cancel out” with the attractive interactions between their oppositely charged parts, resulting in a zero-sum game. However, that intuition turns out to be wrong for reasons explained by a field of study known as statistical mechanics (or statistical thermodynamics), and quantified by what’s called the Maxwell-Boltzmann distribution function, which is well beyond the scope of this post.
The short answer is that nature tends to favor configurations of macroscopic systems which minimize potential energy, thus making them far more statistically probable than other configurations. Interactions between like charges are of higher energy than those between opposite charges.
At higher temperatures, a larger proportion of the molecules in a system can occupy those (otherwise) less energetically-favorable states, but the point is that systems comprised of polar molecules are generally biased toward certain lower energy configurations. They are not totally random, and this has profound effects on their aggregate behavior at larger scales.
Return to Table of Contents:
Go to next section: Ion-dipole interactions and hydrophilicity.
Go to previous section: Ion-ion interactions.