Introduction
In a recent post, I introduced a thermodynamic state function called enthalpy and introduced something called Hess’s Law. That post was following up on two previous posts, the first of which covered the 1st and 2nd Laws of Thermodynamics, entropy, and the distinction between state functions vs path functions, and the second of which covered the concepts of work, heat transfer, reversibility, and internal energy in thermodynamic systems.
Just to recap, enthalpy H is a state function that scientists and engineers use to analyze the thermodynamic properties of certain physical processes (particularly chemical reactions). More accurately, it’s the change in this function that we’re most interested in, particularly at constant pressure, which is the case for most biological processes as well as many experimental situations.
You can check out the previous article for the gory details, but the take home message was that the change in enthalpy at constant pressure is equal to the heat transferred to or from the system, and that its status as a state function led to an important general result called Hess’s Law.
The tl; dr version of Hess’s Law is that the change in enthalpy for a reaction is the sum of the enthalpies of formation of the products, each multiplied by its corresponding coefficient (n) from its balanced chemical equation, minus the enthalpies of formation of the reactants, each (again) multiplied by its corresponding coefficient.
Hess’s Law can also be concisely summarized by the following equation which uses sigma (summation) notation:
This is important to scientists and engineers because it has permitted the tabulation of many experimentally-derived ΔH values under a set of standardized conditions.
Adding and subtracting various combinations of these can facilitate convenient thermodynamic predictions for a wide variety of reactions.
The remainder of this article deals with how Hess’s Law is applied and generalized to a variety of physical situations.
How Are These Ideas Applied?
Returning to equation (8) above: The f subscript denotes that these are enthalpies of formation, meaning the change in enthalpy to form them from their constituent elements. This works because (again) enthalpy is a state function, and therefore path independent, which means that these values can be strung together in different ways to construct the reaction whose change in enthalpy one wishes to calculate.
The 0 superscript denotes that these are standard enthalpies of formation. For explanations of what are considered standard conditions and why, you can read more here and/or here. However, the more important point is that tabulating these values in terms of standard heats of formation makes it possible to generalize this idea to nearly any chemical reaction imaginable, understand its thermodynamic characteristics, and to make predictions on the basis thereof.
This also works well for coupled reactions, which are ubiquitous in biochemistry, and essential to life itself (more on that later). For now, let’s look at an example.
The example in the following graphic depicts the hydrogenation of ethene. Ethene, which is sometimes informally called ethylene, is just two carbons doubled bonded to one another, each with two hydrogens. Hydrogenation is a reaction that students typically learn about in a first semester O-Chem course. It essentially involves adding a hydrogen to each carbon on either side of a carbon-carbon double bond as pictured (in this case resulting in ethane).
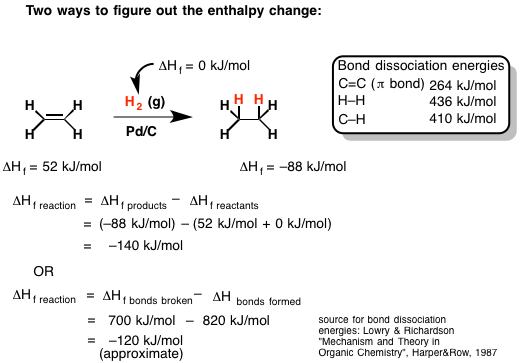
Image c/o Mastering Organic Chemistry
In the above example, James (of Mastering Organic Chemistry) has shown two different ways to predict the enthalpy of this reaction.
The first way requires knowing the experimental standard enthalpies of formation of the reactants and products. The standard enthalpy of formation of the reactants is then subtracted from that of the products (with the appropriate reaction coefficients).
The second way involves estimating the enthalpy of the reaction directly from the bond dissociation energies. Since breaking bonds requires an input of energy (endothermic), the sum of their bond energies are positive, whereas the sum of bond energies of the newly formed bonds is subtracted from that value to yield a rough estimate of the enthalpy change of the reaction.
Heat Capacity and Generalizing to Non-Standard Conditions
The values of ΔH for any given reaction or process vary with temperature and pressure, but here we are primarily talking about conditions of constant (or nearly constant) pressure, and there is an easy way to adjust for temperatures which deviate from the conditions under which the experimental values were tabulated.
Recall that the heat capacity of a substance the amount of thermal energy per unit of the substance required to change its temperature by a given amount. In SI units, this is usually expressed either in joules per Kelvin per gram, or joules per Kelvin per mole, and its value generally fluctuates with temperature at pressure.
However, at constant pressure, if one knows how the heat capacity changes with temperature, it is possible to take the heat capacity as a function of temperature and compute the area under its curve between the standard temperature at which ΔH was tabulated and the temperature of the current experimental situation, and simply add that value to the value of ΔH at tabulated under standard conditions.
As a matter of fact, heat capacity at constant pressure is defined as the change in enthalpy over the change in temperature:
Cp = ΔH/ΔT,
Or in differential form:
dH = CpdT.
So, if you knew the standard state enthalpy change ΔHo of a given reaction at some temperature To, and how the relevant constant pressure heat capacity depended on temperature, and you wanted to know its enthalpy ΔHT at some other temperature (T), it could be computed by evaluating the following equation:
Equation (9) is saying that the change in enthalpy (ΔHT) of some process at some temperature T is equal to the standard state enthalpy (ΔHo) of that process plus the constant pressure heat capacity integrated (with respect to temperature) from the temperature at which the standard state enthalpy was tabulated (To) to the temperature at which it is actually occurring (T).
Notice that if T = To, the limits of integration are both To, which means the integral is equal to zero, in which case this expression would reduce to ΔHTo = ΔHo, which is what we should expect.
Although it is sometimes possible to express the heat capacity as a function of temperature using curve fitting methods from experimental data and then to integrate that function to compute the area under the aforementioned curve, it often requires numerical and/or graphical approximation methods.
Closing thoughts
As I mentioned in the first enthalpy article, my audience base spans the entire spectrum of levels of previous scientific education and depth of interest. Even my most knowledgable readers differ widely in their areas of specialization. This means that any time I reference scientific concepts in future articles, some of my readers will know the topic better than I do, and others will have never heard of it at all.
Rather than extending every future article with compressed summaries of concepts I forsee myself referring to in the future, one of my motivations for writing this post and the three before it was to lay the foundation for other topics I hope to refer back to in future blogs.
One of those topics is called the Gibbs Free Energy, which is ubiquitous in biochemistry and other subcategories of chemistry, biology, and biophysics.
This way, if some readers aren’t familiar with (or forgot about) a scientific concept I refer to in a future article, I can just link to the post in which I explained them instead of extending the new post by taking a detour within it to unpack an idea that was not intended to be the central focus of the piece.
So, stay tuned for an upcoming post on Gibbs Free Energy.
References
Hammes, G. G., & Hammes-Schiffer, S. (2015). Physical chemistry for the biological sciences. John Wiley & Sons.
Burrows, A., Holman, J., Parsons, A., Pilling, G., & Price, G. (2017). Chemistry3: introducing inorganic, organic and physical chemistry. Oxford University Press.
Marcus, R. A. (1997). Transfer reactions in chemistry. Theory and experiment. Pure and applied chemistry, 69(1), 13-30.
Tro, N. J., Fridgen, T., & Shaw, L. (2008). Chemistry: A Molecular Approach, 2e.
Endothermic vs. exothermic reactions. (2018). Khan Academy. Retrieved 7 July 2018, from https://goo.gl/193brE
Hess’s Law. (2013). Chemistry LibreTexts. Retrieved 8 July 2018, from https://goo.gl/4M9ryM
Stoichiometry. (2018). Khan Academy. Retrieved 8 July 2018, from https://goo.gl/KJYWSV
Summation Notation. (2018). Columbia.edu. Retrieved 8 July 2018, from http://www.columbia.edu/itc/sipa/math/summation.html
Learning. (2015). Enthalpy Hess’s Law. Slideshare.net. Retrieved 8 July 2018, from https://www.slideshare.net/CandelaContent/enthalpy-hesss-law
Standard Enthalpy of Formation. (2013). Chemistry LibreTexts. Retrieved 8 July 2018, from https://goo.gl/2Ab9c5
Formation Reactions – Introductory Chemistry- 1st Canadian Edition. (2018). Opentextbc.ca. Retrieved 8 July 2018, from https://opentextbc.ca/introductorychemistry/chapter/formation-reactions-2/
From General Chemistry to Organic Chemistry: Hess’ Law — Master Organic Chemistry. (2018). Masterorganicchemistry.com. Retrieved 8 July 2018, from https://goo.gl/ryPJ1P
Specific Heats. (2018). Grc.nasa.gov. Retrieved 7 July 2018, from https://www.grc.nasa.gov/WWW/K-12/airplane/specheat.html
Lowry, T. H., & Richardson, K. S. (1987). Mechanism and theory in organic chemistry (pp. 143-149). New York: Harper & Row.
T1: Standard Thermodynamic Quantities. (2014). Chemistry LibreTexts. Retrieved 8 July 2018, from https://goo.gl/zrzp1v