Introduction
In a recent article, I talked about the 1st and 2nd Laws of Thermodynamics, entropy, and the distinction between state functions vs path functions.
More recently, I wrote another one in which I talked about heat, work, reversibility, and internal energy in thermodynamic systems.
At the end of the latter post, I mentioned in passing that the path-dependence of heat and work done by non-conservative forces makes it desirable to work with state functions whenever feasible, because it’s not always easy to know the precise path by which a system arrived at its current state from a prior one. That’s where a function called enthalpy comes into play.
Enthalpy
Many laboratory experiments are carried out at constant pressure rather than at constant volume, as are most biological processes. For this reason, scientists defined a state function called enthalpy (denoted simply as H), whereby
H = E + PV (5).
At constant pressure, ΔH = ΔE + PΔV (6),
and ΔE = q – PΔV (by equation (1) from my recent article on heat, work, and internal energy),
in which case an algebraic rearrangement yields
q = PΔV + ΔE (7),
where q again represents heat transfer to or from the system, (and with the same sign convention as outlined in my previous post).
This implies that q = ΔH at constant pressure.
Most1 chemical reactions involve the breaking of certain bonds and the formation of others. Breaking bonds requires an input of energy2, whereas forming new bonds releases energy (Burrows et al 2013). This means that for certain reactions the energy released will exceed the energy absorbed, and for other reactions the opposite will be the case. The question of which wins out depends on the details of the reaction.
Reactions with a negative enthalpy change are called exothermic, meaning they release thermal energy to their surroundings, whereas reactions with a positive enthalpy change are called endothermic, meaning that they absorb heat (cooling their surroundings).
This is particularly useful for studying reactions and processes, not only in general chemistry, but also in biology and biochemistry, because it can be determined experimentally by measuring the heat change at constant pressure, (and because it’s a state function).
Why is this useful?
Hess’s Law
The fact that enthalpy is a state function means that the value of ΔHrxn for a given reaction or process doesn’t depend on the exact sequence of steps by which a reaction proceeded from its reactants to its products. The ΔHrxn values can be added and subtracted for a given sequence of reactions as if the reactions were merely algebraic equations, and neither the number of steps nor their order matters so long as the enthalpy difference between their starting and ending points is known.
So, for any sequence of reactions A → B with ΔH1, B → C with ΔH2, C → D with ΔH3, the ΔH for A → D is just ΔH1 + ΔH2 + ΔH3, regardless of whether that was the sequence of reactions by which D was arrived at from A.
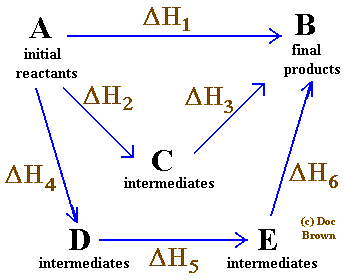
Image source
In the pictured example above, any path from A to B results in the same change in enthalpy:
ΔH1 = ΔH2 + ΔH3 = ΔH4 + ΔH5 + ΔH6
This has allowed for the tabulation of many3 experimentally-derived ΔH values under a set of standardized conditions, combinations of which can be added and subtracted in various ways to facilitate convenient thermodynamic calculations for a wide variety of reactions. Entropy changes have also been tabulated in this manner, (as have changes in Gibbs Free Energy, which I plan to cover in an upcoming installment of this blog).
If one or more of the balanced chemical equations contains stoichiometric coefficients not equal to one, the equation is easily adjusted by placing the appropriate molar coefficient before each value of ΔH.
These are all consequences of what is known as Hess’s Law, which can be concisely summarized by the following equation which uses sigma (summation) notation:
Equation (8) is saying that the change in enthalpy for a reaction is the sum of the enthalpies of formation of the products, each multiplied by its corresponding stoichiometric coefficient (n) from its balanced chemical equation, minus the enthalpies of formation of the reactants, each (again) multiplied by its corresponding stoichiometric coefficient.
*I realize that TCH readers encompass a huge range from beginners and hobbyists to professional research scientists, so if your eyes are already glazing over at the mention of stoichiometry and balanced chemical equations, then you’ll need to review those HS chemistry concepts in order to benefit much from this article, so here’s a quick summary from Khan Academy. While I’m at it, here’s an overview of sigma notation from Columbia University too.
To see how this works, consider the reactions in the graphic below, and their given enthalpy values.

Image c/o Lumen Learning (CC Attribution License)
Notice that the second reaction is just the first reaction multiplied through by ½, and results in half the enthalpy change value as the first reaction. Cutting the amount reacted in half resulted in only half the amount of heat being absorbed.
The third reaction is just the reverse of the first, which is why the enthalpy change is the same except with a negative sign.
Okay, Now What?
Our next step will be to look at how Hess’s Law is applied and generalized to a variety of physical situations.
However, in the interest of keeping these posts from growing longer than desirable, I’ve broken this one up into two parts. In this one, I introduced the concepts of enthalpy and Hess’s Law. In the next one, I’ll unpack what is meant by “standard” enthalpies, parse the difference between the enthalpy of a reaction vs a standard enthalpy of formation, and explain how Hess’s Law can be applied to different reactions, as well as how standard enthalpy values can be modified to accommodate different reaction conditions.
I’m building a foundation right now. I promise that this is going somewhere.
Footnotes
1 I say “most” chemical reactions involve the breaking and forming of bonds because there do exist reactions involving only transfers of electrons without the formation or breaking of chemical bonds.
2 See here for a list of bond dissociation energies.
3 See here for a list of standard enthalpies of formation.
References
Hammes, G. G., & Hammes-Schiffer, S. (2015). Physical chemistry for the biological sciences. John Wiley & Sons.
Burrows, A., Holman, J., Parsons, A., Pilling, G., & Price, G. (2017). Chemistry3: introducing inorganic, organic and physical chemistry. Oxford University Press.
Marcus, R. A. (1997). Transfer reactions in chemistry. Theory and experiment. Pure and applied chemistry, 69(1), 13-30.
Tro, N. J., Fridgen, T., & Shaw, L. (2008). Chemistry: A Molecular Approach, 2e.
Endothermic vs. exothermic reactions. (2018). Khan Academy. Retrieved 7 July 2018, from https://goo.gl/193brE
Hess’s Law. (2013). Chemistry LibreTexts. Retrieved 8 July 2018, from https://goo.gl/4M9ryM
Stoichiometry. (2018). Khan Academy. Retrieved 8 July 2018, from https://goo.gl/KJYWSV
Summation Notation. (2018). Columbia.edu. Retrieved 8 July 2018, from http://www.columbia.edu/itc/sipa/math/summation.html
Learning. (2015). Enthalpy Hess’s Law. Slideshare.net. Retrieved 8 July 2018, from https://www.slideshare.net/CandelaContent/enthalpy-hesss-law
Lowry, T. H., & Richardson, K. S. (1987). Mechanism and theory in organic chemistry (pp. 143-149). New York: Harper & Row.
T1: Standard Thermodynamic Quantities. (2014). Chemistry LibreTexts. Retrieved 8 July 2018, from https://goo.gl/zrzp1v


1 Comment
Applying Hess’s Law, and Generalizing it to Different Physical Situations – The Credible Hulk · July 10, 2018 at 5:14 pm
[…] can check out the previous article for the gory details, but the take home message was that the change in enthalpy at constant […]
Comments are closed.