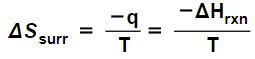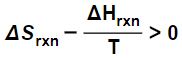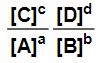Introduction
In my previous couple of blog posts, I talked about a thermodynamic state function called enthalpy, and how it is used by scientists and engineers. This included covering a principle called Hess’s Law, which has led to the tabulation of enthalpy values for certain reactions under a set of standardized conditions, such that the idea could be generalized to make thermodynamic predictions about a huge variety of processes.
Those posts laid the groundwork for the following topic.
Gibbs Energy and Spontaneity
As useful as it is to know whether a process is exothermic or endothermic, a negative enthalpy is neither a necessary nor a sufficient condition to determine whether a process will occur spontaneously. There is another concept in thermodynamics which quantifies the energy associated with a chemical reaction capable of being co-opted to do work, and which tells scientists which reactions or processes will happen spontaneously. It’s particularly ubiquitous in biochemistry, which deals with many complicated multi-step reactions which are favorable under certain conditions, but not others.
In another recent post, I talked about 2nd Law of thermodynamics (among other things), and the idea of conceptually partitioning the universe into a system (in which a reaction or process is occurring) and its surroundings. Recall that the 2nd Law stipulates that the total entropy change of the universe be greater than zero in order for a process to occur spontaneously.
For any given chemical reaction, this implies that
ΔSUniv = ΔSrxn + ΔSsurr > 0 (10) (Tro p. 782)
where ΔSrxn is the change of entropy of the system and ΔSsurr is the change of entropy of the surrounding environment because of the reaction. However, the entropy change of the surroundings due to a reaction at constant temperature in inequality (10) can also be expressed as minus the enthalpy change of the reaction divided by the temperature:
in which case the inequality
ΔSrxn + ΔSsurr > 0
becomes
which can be algebraically rearranged to yield:
0 > ΔH – T ΔS.
If you’re unfamiliar (or just rusty) with the enthalpy concept, see my previous posts here and here.
Here we define a new state function called the Gibbs Free Energy (or simply Gibbs Energy) of the reaction, and is mathematically expressed as
G = H – TS (11)
where G represents the Gibbs Energy, H represents Enthalpy, T represents the temperature at which the reaction or process is occurring, and S represents the entropy (Hammes p. 30). However, usually it’s the change in G at constant T that interests us:
ΔG = ΔH – T ΔS (12).
Here we see that the inequality 0 > ΔH – T ΔS we derived a moment ago is saying that a reaction or process is spontaneous when the Gibbs Free Energy is less than zero.
We call such reactions exergonic.
In contrast, reactions for which ΔG is greater than zero are not spontaneous.
We call such reactions endergonic.
Note that by spontaneous I don’t mean that the processes necessarily occur quickly or abruptly. Spontaneity in this context just means that it will happen on its own without an input of energy. It makes no reference to reaction rates, which is primarily the domain of chemical kinetics.
What about cases for which ΔG = 0?
When the Gibbs term is zero, it means that the rates of the forward and backward reactions or processes are equal, which means that the system is in equilibrium.
Looking at equation 12, you can see that there are only four possibilities for the sign of the terms on the right side of the equation.
Either ΔH is negative while ΔS is positive, in which case ΔG is necessarily negative (and the process is spontaneous), or vice versa, in which case ΔG is necessarily positive (and the process is not spontaneous).
Otherwise, either both ΔH and ΔS are negative, or both are positive, in which case ΔG could be either positive, negative, or zero, depending on the temperature, and the precise magnitudes of ΔH and ΔS.
These cases are concisely summarized in the graphic below.
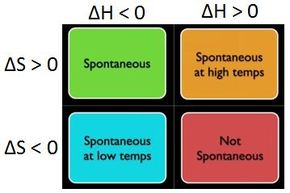
Image source:
As is the case with Enthalpy, Gibbs Free Energy values have been tabulated for a number of common reactions under very specific standardized conditions (usually expressed on a per mol basis), which can be adjusted to accommodate non-standard conditions, and various combinations of which can be added and subtracted to compute free energy changes for even more reactions. The standard state free energy change for a given reaction is denoted ΔG0, where
ΔG0 = ΔH0 – T ΔS0 (13),
and the total free energy change for a reaction is as follows:
Where the ΔG0 values of each product and reactant is multiplied by its appropriate coefficient from the reaction’s balanced chemical equation.
Free Energy and Chemical Equilibria
A chemical reaction is said to have reached equilibrium when the rate of the backward reaction equals the rate of the forward reaction. This point of equilibrium is characterized by a ratio of products to reactants, which in turn is determined by the thermodynamic details of the specific reaction in question.
This ratio is usually denoted as simply K. Its numeric value of also depends on temperature, which should make sense if you recall that temperature determines the extent to which the entropy change term affects the change in Gibbs energy equation. Stare at equation 12 for a while if it’s not clear why that’s the case.
You may or may not recall from High School chemistry that for any reaction of the form
aA + bB ↔ cC + dD,
when the reaction reaches equilibrium, the equilibrium constant K can be expressed as
You may or may not recall that there was also another similar-looking value called the reaction quotient, Q, such that
when the reaction is not at equilibrium.
Moreover, sometimes we want to know the direction a reaction will go when it is not in equilibrium, in which case the Gibbs free energy equation is adjusted such that
ΔG = ΔG0 + RT*ln(Q) (17).
What this relation tells us is that the spontaneity of a reaction (or lack thereof) depends not only on the standard state free energy, but also on the relative concentrations of substrates and products at any given time. There are three main cases to consider here:
Q < K,
Q > K, and
Q = K.
If Q is less than K, then the concentrations of the products are lower (relative to reactants) than they would be at equilibrium, and therefore the forward reaction is favored.
If Q is greater than K, then the concentrations of the products are higher (relative to reactants) than they would be at equilibrium, and therefore the reverse reaction in favored.
When Q reaches K, the reaction is in equilibrium which means that ΔG = 0, in which case
0 = ΔG0 + RT*ln(K),
from which we discover the useful relation that ΔG0 = – RT*ln(K).
This also gives us a thermodynamic justification for at least one aspect of Le Chatelier’s principle. Namely, it quantifies the way in which the addition or removal of reactants or products to or from a reaction mixture leads to a shift in their relative concentrations to oppose the change. So long as the temperature remains constant, the ratio of products and reactants at equilibrium depicted in equation 15 is still valid, but the concentrations of reactants and products are shifted in order to re-establish that equilibrium.
This dependence of a reaction’s spontaneity on relative substrate concentrations is one of the ways in which biological organisms naturally perform many processes that would otherwise superficially seem improbable in the absence of outside intervention (divine or otherwise). Another way is through the coupling of an endergonic reaction with an exergonic one.
However, in the interest of keeping these posts to a digestible length, I’m planning to cover that in a subsequent post, as well as recapping the salient points of this one and clarifying them with a couple of specific examples. Stay tuned.
References
Tro, N. J., Fridgen, T., & Shaw, L. (2008). Chemistry: A Molecular Approach, 2e
Tymoczko, J. L., Berg, J. M., & Stryer, L. (2011). Biochemistry: a short course. Macmillan.
Hammes, G. G., & Hammes-Schiffer, S. (2015). Physical chemistry for the biological sciences. John Wiley & Sons.
Le Chatelier’s Principle. (2018). Chemguide.co.uk. Retrieved 10 July 2018, from https://www.chemguide.co.uk/physical/equilibria/lechatelier.html
Berg, J. M., Tymoczko, J. L., & Gatto Jr, G. J. (2002). Stryer, L: Biochemistry. Section 8.2, Free Energy Is a Useful Thermodynamic Function for Understanding Enzymes. W.H. Freeman and Company, 5, 306-307. Available from: https://www.ncbi.nlm.nih.gov/books/NBK22584/