Electrostatics
Recall that electrostatics is the study of stationary electric charges. Charged particles are characterized as either positive or negative. Like charges repel, whereas opposite charges attract. Symmetries in the laws of electromagnetism imply that these roles could be reversed with minimal consequence to our theoretical understanding or its pertinence to the empirical world. In that sense, the establishment of which one is positive and which is negative is admittedly somewhat arbitrary, and is therefore mostly a matter of convention.
Be that as it may, the presence of electric charges generates an electric field, and the electrostatic force of one charge on another is governed by an inverse square relationship commonly expressed as Coulomb’s Law:
F = Kq1q2/r2,
where q1 and q2 represent electric charges, r represents the distance between them, and K is a constant (called the Coulomb constant), which in SI units is approximately equal to 8.99*109 N*m2/kg2.
In some representations, K will be expressed as , where εo is a constant called the Permittivity of Free Space, which in SI units is equal to approximately 8.85*10-12 C2/N*m2, but I will usually use K for our purposes here.
If only those two charges are involved, then the electrostatic force acts along the straight line adjoining the two charges, and does so with a magnitude proportional to the product of their respective electric charges, and inversely proportional to the square of the distance between them.
If both charges are positive or both negative, then the force one exerts on the other is positive (pushing it further away), whereas if one charge is positive and the other negative, the force one exerts on the other is negative (pulling it towards the source of the charge).
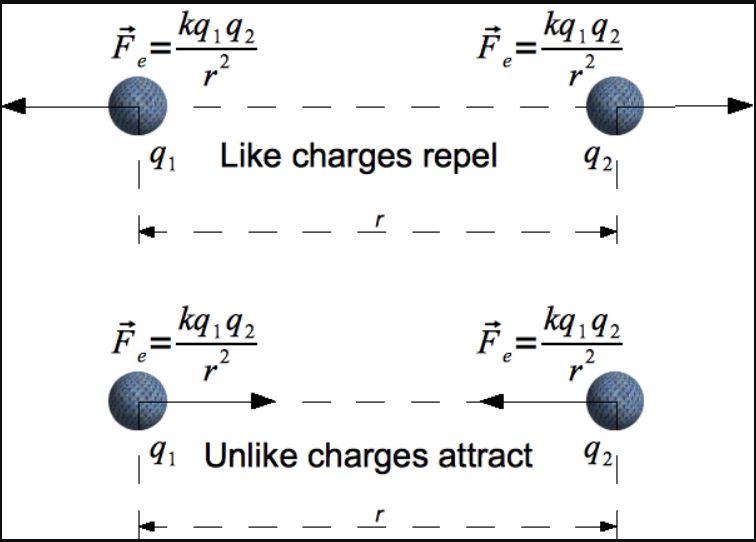
Image source:
If there are many charges involved, things get more complicated, but the net result for the electrostatic force on one charge due to a whole bunch of other charges is the vector sum of all the Coulomb forces from all the other charges acting on the particle of interest. See here for my brief intro to vectors.
In practice, this is rarely done. Instead, a concept is introduced called an electric field. An electric field is a vector field with a magnitude and a direction at each point in space, and whose magnitude at a given point represents the force per unit charge that a positively charged “test” particle would experience at a given point if it happened to be at that point. There are convenient mathematical devices for computing electric fields from a charge distribution in a region of space, such as Gauss’s Law.
Obviously, this gets a lot more complicated when those forces accelerate said charges, thus changing their relative positions. However, insofar as understanding intermolecular forces, the point is that these forces depend on the charges of the atoms, ions, or molecules of interest, and their relative distances from one another.
Return to Table of Contents:
Go to next section: Ion-ion interactions.