State Functions, Entropy, Path Dependence, and Energy Conservation in Thermodynamic Systems

State Functions vs Path Dependent Functions

In thermodynamics, scientists distinguish between what are called state functions vs path functions. State functions are properties of a system whose values do not depend on how they were arrived at from a prior state of the system. They depend only on the starting and ending states of the system. On the other hand, path functions can take on very different values depending on the path by which the system arrived at a state from its previous state.

For example, there are probably a few different ways you could get from your house to your friend’s house across town, all of which would result in the same displacement between your home and your friend’s. However, some of those paths would be less direct than others, and would therefore require you to travel a greater path length (and spend more on gas if you’re driving).

The displacement is therefore a state function, whereas the path length (and gas required) depends on the path taken. Examples of thermodynamic state functions include temperature, pressure, internal energy, density, entropy, and enthalpy. Examples of path dependent thermodynamic variables include heat and work.

System vs surroundings and the Laws of Thermodynamics

One of the fundamental concepts of thermodynamics is the idea of dividing the universe into a system + its surroundings. In this way, scientists and engineers can choose to define the boundaries between the environment and the system they are analyzing in a way that makes it convenient to apply the 1^st and 2^nd Laws of Thermodynamics to them both.

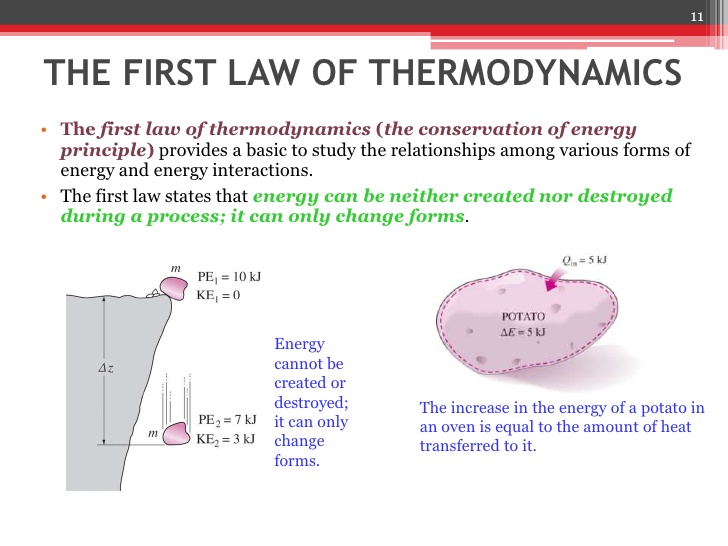
The 1^st Law: Conservation of Energy

The 1^st Law is just the law of conservation of energy, which states that the total energy of an isolated system is constant. It is often conveyed by the statement that energy can be neither created nor destroyed in an isolated system, but rather can only change from one form of energy to another.

Image source:

This means that changes in the internal energy of a thermodynamic system are compensated for by the surroundings such that the total energy of the universe is conserved. An increase in a system’s internal energy requires an input of heat and/or work from the surrounding environment, whereas a decrease requires a release of heat from the system to the environment, and/or work done by the system on the environment.

*As an interesting (albeit admittedly tangential) side-note, energy-momentum conservation is not so well-defined for certain cosmological applications of general relativity. See footnote at the end of this article.

Entropy and the 2^nd Law

The 2^nd Law is a little subtler, and can be stated and explained in different (albeit ultimately equivalent) ways, either in terms of classical or statistical thermodynamics.

For example, the Clausius statement of the 2^nd Law is that

“No process is possible whose sole result is the transfer of heat from a cooler to a hotter body,”

whereas the Plank-Kelvin formulation of the 2^nd Law is stated as follows:

“No process is possible whose sole result is the absorption of heat from a reservoir and the conversion of this heat into work.”

For the purposes of this section, however, the 2^nd Law can be thought of as stating that the total disorder of the universe (entropy) tends to increase over time. Energy is still conserved, but over time, less of it is available to do work. So, if the entropy of a system decreases (becomes more ordered), then that will be compensated for by an increase in the entropy (or disorder) of the surroundings, and vice versa.

Note that although the loose definition of entropy as a measure of disorder suffices for the purposes of this discussion, it is not strictly correct. In classical thermodynamics, the details of a system’s constituents are not considered, but are instead described by their macroscopically averaged behavior. Definitions of the properties of thermodynamic systems were also presumed to be in equilibrium, and were only much later extended to non-equilibrium situations. From this view, entropy represents the amount of energy per unit temperature of a system that is unavailable to do useful work.

In statistical mechanics, the entropy of a system is defined in terms of the statistics of the motions of its constituent particles. Namely, for a given macrostate of a system, its entropy is given by k_Bln(Ω), where k_B is called the Boltzmann constant, which is equal to 1.38*10^-23 Joules per Kelvin in SI units, and Ω represents the number of possible microstates of the particles that together would comprise the same macrostate – a concept which relies on the indistinguishability of certain configurations of identical particles. This has since even been extended to incorporate quantum statistics.

Another description of entropy I like, one which is particularly applicable to information theory, was one I stumbled across in an article by Johannes Koelman (the Hammock Physicist). Johannes stated it thusly:

“The entropy of a physical system is the minimum number of bits you need to fully describe the detailed state of the system”

If all of that seems too confusing, don’t worry about it. Trust me. You’re not alone. Instead, just think of entropy as a measurement of randomness or disorder for now. For more on entropy and the 2^nd Law, see here.

Lord Entropy: an anthropomorphized comic personification of the Entropy concept (just because this awesome song about him by my friends Tombstone da Deadman and Greydon Square wouldn’t stop replaying in my head while I was writing that last section).😎 

I intend to refer back to these ideas in a separate article in which I plan to unpack the concepts of heat, work, and internal energy. The following section on conservation of energy in GR is not directly pertinent to that goal, but is just a tangential issue I thought was cool enough to mention for the benefit of any of my readers as fascinated as I am with the science of cosmology.

*More on energy conservation in relativistic cosmology: For example, the red shift of the Cosmic Microwave Background Radiation (CMB) due to universal expansion entails that the photons must lose energy over time, because longer wavelengths correspond to lower energies, and it’s not clear whether (and/or the sense in which) that energy might be compensated for as gravitational potential energy.

Needless to say, adding dark energy into the mix doesn’t exactly make this any clearer. This has led some physicists and cosmologists, including popular science communicator extraordinaire, Sean Carroll, to say that the total energy of the universe isn’t conserved; “it changes because spacetime does.”

The Law is sometimes reformulated in General Relativity as the statement that the covariant derivative of the stress-energy tensor is equal to zero in all reference frames. But what this means insofar as how we ought to conceptualize physical reality is not clear, and is further confounded by differences in the transformation rules governing mathematical objects called tensors, whose equations are valid in all possible coordinate systems (if they’re valid in any), vs so-called pseudo-tensors, which arise in certain models, but whose usefulness is contingent upon the scientist’s choice of coordinate systems.

To be clear, none of this has to do with any disagreement among physicists as to what is actually happening physically. Rather, it’s a matter of how best to translate certain implications of GR into conceptually intelligible terms for people not intimately familiar with the mathematical details of the theory. To quote Sean Carroll once again,

“All of the experts agree on what’s happening; this is an issue of translation, not of physics. And in my experience, saying “there’s energy in the gravitational field, but it’s negative, so it exactly cancels the energy you think is being gained in the matter fields” does not actually increase anyone’s understanding — it just quiets them down. Whereas if you say, “in general relativity spacetime can give energy to matter, or absorb it from matter, so that the total energy simply isn’t conserved,” they might be surprised but I think most people do actually gain some understanding thereby.”

References

State vs. Path Functions. (2018). Chemistry LibreTexts. Retrieved 2 July 2018, from https://goo.gl/eoEQBd

Feynman, R. P., Leighton, R. B., & Sands, M. (2011). The Feynman lectures on physics, Vol. I: The new millennium edition: mainly mechanics, radiation, and heat (Vol. 1). Basic books.

Weiss, M., & Baez, J. (2017). Is Energy Conserved in General Relativity?. (2018). Math.ucr.edu. Retrieved 2 July 2018, from http://math.ucr.edu/home/baez/physics/Relativity/GR/energy_gr.html

5.1 Concept and Statements of the Second Law. (2018). Web.mit.edu. Retrieved 2 July 2018, from http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node37.html

An introduction to thermodynamics. (2018). Google Books. Retrieved 2 July 2018, from https://books.google.com/books?id=iYWiCXziWsEC&pg=PA213#v=onepage&q&f=false

A Course in Classical Physics 2—Fluids and Thermodynamics. (2018). Google Books. Retrieved 2 July 2018, from https://goo.gl/Y9A6Sv

Equilibrium Thermodynamics. (2018). Google Books. Retrieved 2 July 2018, from https://goo.gl/qiq56n

Entropy | Definition and Equation. (2018). Encyclopedia Britannica. Retrieved 2 July 2018, from https://www.britannica.com/science/entropy-physics

Microstates. (2018). Chemistry LibreTexts. Retrieved 3 July 2018, from https://goo.gl/VQNCkU

Entropy?, W. (2018). What Is Entropy?. Science 2.0. Retrieved 3 July 2018, from http://www.science20.com/hammock_physicist/what_entropy-89730

Entropy. (2013). Chemistry LibreTexts. Retrieved 3 July 2018, from https://goo.gl/ZTJ6WR

Energy Is Not Conserved. (2010). Sean Carroll. Retrieved 3 July 2018, from http://www.preposterousuniverse.com/blog/2010/02/22/energy-is-not-conserved/