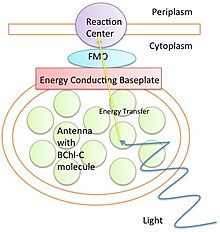
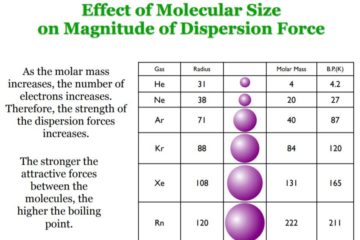
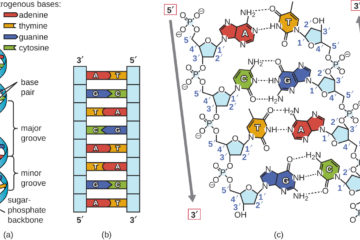
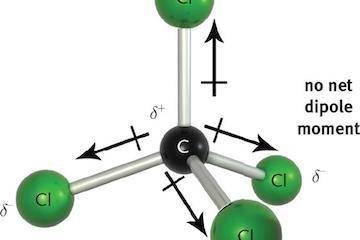
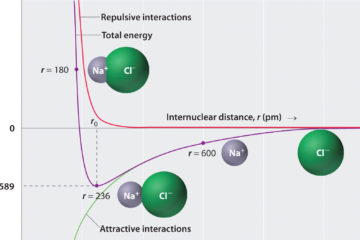
The “Scientists Were Wrong” Gambit and the Science Denier’s Paradox
Introduction It’s no secret that humans are not always rational. Although innately possessing the capacity for complex and abstract reasoning, strongly-held beliefs and cognitive biases often lead people to use that ability selectively and/or to employ it in the defense Read more…