Uncategorized

Free Energy, Relative Substrate Concentrations, and Coupled Reactions in Biochemistry

Introduction

In a recent article, I introduced the concept of the Gibbs energy of a chemical reaction. Before building on the content of that post, I’d like to recap its most salient points:

Gibbs energy change is an important and broadly applicable thermodynamic concept which provides a reliable way of determining the conditions under which specific reactions or processes will occur spontaneously.

Gibbs energy change values have been tabulated for many different reactions under standardized conditions. Since it’s a state function, various linear combinations of those values can be added and subtracted like algebraic equations to calculate the values of still other reactions.

As was the case with enthalpy, (which I covered here and here), there exist ways of adjusting those standardized values so that they still yield viable answers under non-standard reaction conditions.

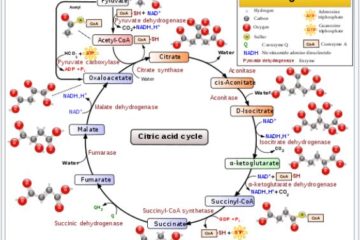
The Gibbs energy of a reaction is closely tied with its equilibrium constant (K), whose numeric value represents the ratio of products to reactants at which the reaction equilibrates at a given temperature.

This provides a thermodynamic explanation for why the relative concentrations of substrates for a given reaction affects whether it will occur spontaneously (and to what extent).

In turn, this dependence of a reaction’s spontaneity on relative substrate concentrations is one of the ways in which biological organisms naturally perform many processes that would otherwise be thermodynamically unfavorable.

My goal for this post is to use a couple of examples to illustrate how the spontaneity of some biochemical processes can be affected by relative substrate concentrations, and/or by the coupling of an endergonic (non-spontaneous) process with an endergonic (spontaneous) one. (more…)

Share
By Credible Hulk, ago

The One True Argument™

Anyone who has spent much time addressing a lot of myths, misconceptions, and anti-science arguments has probably had the experience of some contrarian taking issue with his or her rebuttal to some common talking point on the grounds that it’s not the “real” issue people have with the topic at hand. It does occasionally happen that some skeptic spends an inordinate amount of time refuting an argument that literally nobody has put forward for a position, but I’m specifically referring to situations in which the rebuttal addresses claims or arguments that some people have actually made, but that the contrarian is implying either haven’t been made or shouldn’t be addressed, because they claim that it’s not the “real” argument. This is a form of No True Scotsman logical fallacy, and is a common tactic of people who reject well-supported scientific ideas for one reason or another. In some cases this may be due to the individual’s lack of exposure to the argument being addressed rather than an act of subterfuge, but it is problematic regardless of whether or not the interlocutor is sincere. (more…)

Share
By Credible Hulk, ago

Mean Field Theory and Solar Dynamo Modeling

In a recent post, I talked about the characteristics of the sun’s 11 and 22 year cycles, the observed laws which describe the behavior of the sunspot cycle, how proxy data is used to reconstruct a record of solar cycles of the past, Grand Solar Maxima and Minima, the relationship between Total Solar Irradiance (TSI) and the sunspot cycle, and the relevance of these factors to earth’s climate system. In a follow up post, I went over the structure of the sun, and some of the characteristics of each layer, which laid the groundwork for my last post, in which I explained the solar dynamo: the physical mechanism underlying solar cycles.

Before elaborating on the sun’s role in climate change in the installment following this one, I’ll be going over an approach called “Mean Field Theory” in this installment, which dynamo theorists and other scientists sometimes use to make the modelling of certain systems more manageable. As was the case with part III, this may be a bit more technical than most of my subscribers are accustomed to, but I think the small subset of readers with the tools to digest it will appreciate it. And to be perfectly blunt, writing this was not just about my subscribers. I wanted to do it. It was an excuse for me to dig more deeply into something that has been going on in modern stellar astrophysics that I thought was interesting. The fact that it happened to be tangentially related to my series on climate science was a mere convenience. Anyone wanting to avoid the math and/or to cut to the chase with respect to the effects of solar cycles on climate change might want to skip ahead to part V, or perhaps just read only the text portions of this post. However, for those who don’t mind a little bit of math, I present to you the following: (more…)

Share
By Credible Hulk, ago